Schwerpunkte
Die Mitglieder des Instituts für Industriemathematik betreiben Spitzenforschung in den unterschiedlichsten Bereichen der angewandten Mathematik. Die Kernkompetenzen der einzelnen Mitglieder sind:
In Bearbeitung
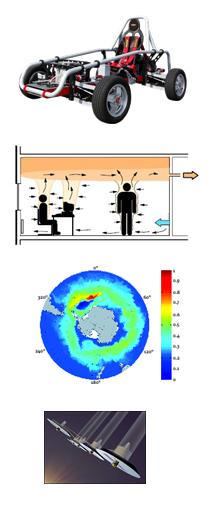
Unter einem dynamischen System versteht man ein System, welches sich mit der Zeit verändert. Diese Systeme treten praktisch in allen Anwendungen auf, z.B. in der Fahrzeugdynamik, bei der Raumklimatisierung, in der Atmosphäre oder in der Astrodynamik. Mithilfe numerischer Methoden lassen sich das Kurzzeit- sowie das Langzeitverhalten solcher Systeme vorhersagen. Somit können dynamische Effekte wie z.B. das Schwingungsverhalten untersucht und beeinflusst werden.
In Bearbeitung
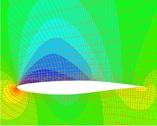
In fast allen Anwendungen sind heutzutage mehrere Ziele von Interesse. In einem Produktionsprozess sollen beispielsweise gleichzeitig die Qualität maximiert und die Herstellungskosten minimiert werden. Beim autonomen Fahren möchte man gleichzeitig schnell und energieeffizient fahren. Moderne mathematische Methoden ermöglichen es, die Menge optimaler Kompromisse (die sogenannte Paretomenge) zwischen den miteinander konkurrierenden Zielfunktionen zu berechnen. So lassen sich intelligente Systeme entwickeln, die auf ihre Umgebung reagieren und je nach den Wünschen des Betreibers ihre Ziele anpassen können.
Viele Optimierungsverfahren benutzen Ableitungsinformationen, um Optima zu berechnen. Diese lassen sich für komplexe Anwendungen häufig nur sehr schwer analytisch berechnen. Mithilfe des Algorithmischen Differenzieren ist es möglich, Ableitungsinformationen direkt aus dem Simulationscode zu gewinnen. Durch Strukturausnutzung und Parallelisierung lassen sich so auch für sehr komplexe Probleme effiziente Optimierungsverfahren entwickeln.